This is a very common scenario in low speed crashes: a patient is injured, the car shows little or no vehicle damage, and the defense expert testifies that, based on his calculations, the acceleration that the occupant experienced during the crash was minor and that injury was impossible.
The expert’s testimony may be very impressive to a jury, since his or her report seems to be very authoritative and accurate—“the occupant did not experience an acceleration greater than 3.12 Gs.”
The truth is that these numbers are not accurate—in fact, they are virtually pulled out of thin air. Understanding how the engineering expert determines these numbers is critical, because once we understand how to calculate the acceleration of a collision, we can see that it is impossible to do so accurately by simply observing photos of the cars after the crash.
First, it is possible to calculate the acceleration that the target vehicle (or the vehicle that is struck during a collision) experiences, but you need to have some very important pieces of information before you can do so. This equation is used to calculate the velocity of the target vehicle:
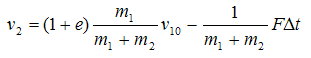
Where,
v2 = increase in velocity of the target vehicle after the collision.
v10 = closing velocity before the collision.
e = coefficient of restitution.
m1 = mass of the bullet vehicle.
m2 = mass of the target vehicle.
F = sum of the external forces on the two vehicles (e.g., braking force and rolling resistance).
Δt= Delta t, or the length of time in which the impact takes place.
We can calculate the final velocity of the target vehicle, or v2, if we know the mass of the bullet and the target vehicles, the closing velocity of the bullet vehicle, or v10, and the coefficient of restitution of the collision. The coefficient of restitution simply measures the elasticity of the collision, or how much bounce the cars exhibit when they collide. The coefficient of restitution is calculated as follows:
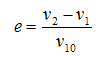
Where,
v2 = velocity of the target vehicle after the collision.
v1 = velocity of the bullet vehicle after the collision.
v10 = closing velocity of the bullet vehicle before the collision.
Let’s just go down the list, and look at the problems that face the accident reconstructionist (AR). (Next page)